ความแม่น (accuracy) เป็นคุณลักษณะที่ชี้ว่าผลการทดสอบมีค่าใกล้ค่าจริง (true value หรือ trueness) หรือค่าอ้างอิง (reference value) หรือค่าที่ยอมรับ (accepted value) ความแม่นแสดงโดยความใกล้เคียงกันระหว่างค่าที่ได้จากการวิเคราะห์กับค่าจริง หรือค่าที่ยอมรับ เนื่องจากในทางปฏิบัติยากที่จะทราบค่าจริง จึงใช้วิธีเปรียบเทียบกับค่าที่ยอมรับแทน โดยทั่วไปความแม่นจะสัมพันธ์กับค่าความเอนเอียง (bias) หรือความคลาดเคลื่อน การตรวจสอบความแม่นของวิธีมักรายงานด้วยร้อยละการกลับคืน (recovery) วิธีที่มีค่าร้อยละการกลับคืนใกล้เคียง 100% ถือว่าวิธีมีความแม่นสูง [ISO5725-2:2019]
การประเมินและยอมรับความแม่นสามารถดำเนินการได้ 2 แบบดังนี้
แบบที่ 1 กรณีมีวัสดุอ้างอิง (RM) หรือวัสดุอ้างอิงรับรองค่า (CRM) ทำดังนี้
(1) ให้ทดสอบวัสดุอ้างอิง หรือวัสดุอ้างอิงรับรองค่า (CRM) อย่างน้อย 3 ความเข้มข้น คือ ความเข้มข้นที่ใกล้เคียงค่าต่ำ กลาง และสูง หรือระดับความเข้มข้นที่ LOQ (ถ้ามีการหา LOQ) และ/หรือ 0.5 เท่า, 1.0 เท่า และ 1.5 เท่า (หรือ 2.0 เท่า) ของค่าความเข้มข้นที่กำหนด (target concentration) เช่น ค่าที่กำหนดตามกฎหมาย แต่ละความเข้มข้นทดสอบไม่น้อยกว่า 10 ซ้ำ
(2) ทำการทดลองหรือทดสอบตามวิธีที่ใช้ในการวิเคราะห์สารตัวอย่าง คำนวณหาค่าเฉลี่ยของแต่ละความเข้มข้น
(3) เกณฑ์การยอมรับ ให้เลือกวิธีใดวิธีหนึ่ง ดังนี้
-
- วิธีที่ 1 ค่าเฉลี่ยที่ได้จากการทดลองมีค่าอยู่ในช่วงของค่ารับรอง เช่น ค่ารับรองมีค่า 40.00±0.15% ค่าเฉลี่ยที่ได้จากการวิเคราะห์วัสดุอ้างอิงต้องอยู่ในช่วง 39.85% ถึง 40.15% ถ้าได้ค่าเฉลี่ยในช่วงดังกล่าวนี้ แสดงว่าวิธีทดสอบมีความแม่นสูง แต่ถ้าค่าเฉลี่ยที่ได้ไม่ได้อยู่ในช่วง ต้องพิจารณาด้วยวิธีที่ 2 คือใช้สถิติทดสอบค่าเฉลี่ย
- วิธีที่ 2 ใช้สถิติทดสอบค่าเฉลี่ย โดยใช้สถิติทดสอบ t-test เปรียบเทียบค่าเฉลี่ยของวิธีทดสอบกับค่าอ้างอิงแตกต่างกันอย่างมีนัยสำคัญที่ระดับความมั่นใจที่กำหนดหรือไม่
แบบที่ 2 กรณีไม่มีวัสดุอ้างอิงรับรองค่า ให้เตรียมสารที่มีเมทริกซ์ (matrix) ใกล้เคียงกับสารตัวอย่าง ซึ่งเรียกว่า สารตัวอย่างควบคุมคุณภาพ (quality control sample, QC) แล้วทำการเติมสารมาตรฐานของสารที่สนใจที่ทราบปริมาณแน่นอนลงไปปริมาณน้อย ๆ เรียกว่า ตัวอย่างเติมสารมาตรฐาน (spiked sample หรือ fortified sample) ทำการวิเคราะห์ตามขั้นตอนแล้วคำนวณหาร้อยละการกลับคืน (%recovery) ทำดังนี้
(1) นำ spiked sample และสารตัวอย่างที่ไม่เติมสารมาตรฐาน (unspiked sample) ทดสอบตามวิธีวิเคราะห์อย่างน้อย 3 ความเข้มข้น คือ ความเข้มข้นที่ใกล้เคียงค่าต่ำ กลาง และสูง หรือระดับความเข้มข้นที่ LOQ (ถ้ามีการหา LOQ) และ/หรือ 0.5 เท่า, 1.0 เท่า และ 1.5 เท่า (หรือ 2.0 เท่า) ของค่าความเข้มข้นที่กำหนด (target concentration) แต่ละความเข้มข้นทดสอบไม่น้อยกว่า 10 ซ้ำ
(2) คำนวณหาร้อยละการกลับคืนของการทดสอบแต่ละซ้ำ ดังนี้
เมื่อ
C1 = ความเข้มข้นที่วัดได้จากสัญญาณของ spiked sample
C2 = ความเข้มข้นที่วัดได้จากสัญญาณของ unspiked sample
C3 = ความเข้มข้นของสารมาตรฐานเติม
(3) คำนวณค่าเฉลี่ยของร้อยละการกลับคืนจากการทดสอบ 10 ซ้ำนำไปเปรียบเทียบผลกับเกณฑ์ที่ยอมรับ
(4) เกณฑ์การยอมรับขึ้นอยู่กับความเข้มข้นของตัวอย่าง ตัวอย่างเกณฑ์ยอมรับของร้อยละการกลับคืนเพื่อใช้เป็นแนวทางในการทดสอบน้ำและน้ำทิ้ง แสดงในตารางที่ 3 และการเกณฑ์ยอมรับตามมาตรฐานทางอาหารและยาแสดงในตารางที่ 4
ตารางที่ 3 เกณฑ์การยอมรับของร้อยละการกลับคืนตามมาตรฐานการทดสอบน้ำและน้ำทิ้ง
| พารามิเตอร์ | %recovery |
| กรด (acid) | 60-140 |
| ไอออนลบ (anion) | 80-120 |
| เบสหรือสารที่เป็นกลาง (base or neutral) | 70-130 |
| ยาฆ่าแมลงคาร์บาเมต (carbamate) | 50-150 |
| ยาฆ่าวัชพืช (pesticide) | 40-160 |
| โลหะ (metal) | 80-120 |
ตารางที่ 4 เกณฑ์การยอมรับของร้อยละการกลับคืนตามมาตรฐานทางอาหารและยา. (AOAC, 2002).
| ความเข้มข้น | %recovery |
| 100% | 98-101 |
| 10% | 95-102 |
| 1% | 92-105 |
| 0.1% | 90-108 |
| 0.01% | 85-110 |
| 10 mg/g (ppm) | 80-115 |
| 1 mg/g (ppm) | 75-120 |
| 10 mg/kg (ppb) | 70-125 |
เกณฑ์การยอมรับตามตารางข้างต้น เป็นเพียงแนวทางเท่านั้น ห้องปฏิบัติการอาจปรับตามความเหมาะสม หรือตามค่าอ้างอิงเฉพาะของการทดสอบแต่ละด้าน เกณฑ์ค่ากลางๆ ทั่วไปแนะนำให้อยู่ที่ 80%-120% และถ้าตรวจสอบแล้วได้ค่าต่ำกว่า 60%-70% หรือสูงกว่า 120% ควรปรับปรุงวิธีใหม่
ความเที่ยง (precision) หรืออาจเรียกว่าความแม่นยำ เป็นคุณลักษณะที่แสดงความสามารถในการทดสอบตัวอย่างซ้ำหลาย ๆ ครั้งแล้วให้ผลใกล้เคียงกัน ความเที่ยงแสดงความใกล้เคียงกันระหว่างค่าที่ได้จากการวิเคราะห์ตัวอย่างเดียวกันจากการทดสอบซ้ำหลาย ๆ ครั้ง ภายใต้เงื่อนไขที่ถูกระบุไว้ของการทดสอบ ซึ่งคำที่จะแสดงค่าความเที่ยงในวิธีทดสอบต่าง ๆ มักใช้คำว่า การทวนซ้ำได้ของการวัด (repeatability) และ การทำซ้ำได้ของการวัด (reproducibility) อย่างไรก็ตาม ความเที่ยงไม่ได้บอกถึงความแม่นของผลการทดสอบแต่อย่างใด แต่เป็นค่าที่บ่งชี้ว่าการทดสอบมีความสม่ำเสมอ เที่ยงตรงในระดับใดเมื่อมีการทดสอบซ้ำหลาย ๆ ครั้ง โดยทั่วไปเงื่อนไขที่ถูกระบุของการการวัดความเที่ยงแบ่งได้ 3 ระดับคือ
1) เงื่อนไขการทวนซ้ำได้ของการวัด (repeatability) เป็นสภาวะการทดสอบที่ทำในสภาวะเดิมทั้งหมด การวิเคราะห์ซ้ำที่ทำในสภาวะเดียวกัน เงื่อนไขของการวัดหนึ่งจากชุดของเงื่อนไขต่าง ๆ ที่รวมถึงวิธีดำเนินการวัดเดียวกัน ตัวอย่าง ผู้ปฏิบัติงานคนเดียวกัน ระบบวัดเดียวกัน ภาวะปฏิบัติงานเดียวกัน และสถานที่ปฏิบัติงานเดียวกัน และการวัดซ้ำหลายๆ ครั้งบนวัตถุเดิมหรือที่มีลักษณะคล้ายเดิมในช่วงระยะเวลาสั้นๆ ระยะหนึ่ง จากการตรวจสอบสภาวะแบบนี้ชี้ให้เห็นคุณลักษณะวิธีได้ แต่ไม่สามารถใช้ควบคุมสภาวะการทดสอบระยะยาวได้
2) เงื่อนไขความเที่ยงระดับกลางของการวัด (intermediate precision) คือการแสดงความเที่ยงของการวิเคราะห์ชุดการวิเคราะห์ที่ทำซ้ำโดยมีเงื่อนไขของการวัดหนึ่งจากชุดของเงื่อนไขต่าง ๆ ที่รวมถึงวิธีดำเนินการวัดเดียวกัน ผู้ปฏิบัติงานคนเดียวกัน ระบบวัดเดียวกัน ภาวะปฏิบัติงานเดียวกันและสถานที่ปฏิบัติงานเดียวกัน และการวัดซ้ำหลายๆ ครั้งบนวัตถุเดิมหรือที่มีลักษณะคล้ายเดิมในช่วงระยะเวลาระยะหนึ่งที่ไม่สั้นจนเกินไป แต่อาจรวมถึงเงื่อนไขอื่นที่เกี่ยวข้องกับการเปลี่ยนแปลง เช่น เปลี่ยนผู้ทดสอบ เพื่อให้ครอบคลุมการเปลี่ยนแปลงที่อาจเกิดขึ้นในสภาวะการทำงานจริง ข้อมูลที่ได้สามารถนำไปใช้ควบคุมคุณภาพการทดสอบในระยะยาวของห้องปฏิบัติการได้
3) เงื่อนไขการทำซ้ำได้ของการวัด (reproducibility) คือการแสดงความเที่ยงของการวิเคราะห์ที่เงื่อนไขของการวัดหนึ่งจากชุดของเงื่อนไขต่าง ๆ ที่รวมถึงสถานที่ที่ต่างกัน ผู้ปฏิบัติงานที่ต่างกัน ระบบวัดที่ต่างกันและการวัดซ้ำหลายๆ ครั้งบนวัตถุเดิมหรือที่มีลักษณะคล้ายเดิม
3.1) Intra-lab reproducibility หมายถึง การทดสอบซ้ำโดยอาจจะขยายเวลาในการทดสอบมากขึ้น มีการเปลี่ยนแปลงเจ้าหน้าที่ทดสอบ เปลี่ยนเครื่องมือ วันที่ทำการทดสอบต่างกัน แต่ห้องปฏิบัติการที่ใช้ทดสอบเป็นห้องปฏิบัติการเดียวกัน
3.2) Inter-lab reproducibility หมายถึง การทดสอบซ้ำโดยดูค่าความแปรปรวนที่มีผลต่อความเที่ยงของวิธีเมื่อมีการเปลี่ยนผู้ทดสอบ เปลี่ยนเครื่องมือ แต่ไม่ได้ทำการทดสอบโดยห้องปฏิบัติการเดียวกัน
ความเที่ยงการวัดโดยทั่วไปถูกแสดงด้วยตัวเลขซึ่งบอกขนาดของความไม่เที่ยง เช่นค่าเบี่ยงเบนมาตรฐาน (standard deviation; s) ค่าความแปรปรวน (variance; s2) หรือ สัมประสิทธิ์ความแปรปรวน (coefficient of variation; CV) หรือค่าส่วนเบี่ยงเบนมาตรฐานสัมพัทธ์ (relative standard deviation; RSD) ซึ่งเกี่ยวกับการความคลาดเคลื่อนแบบสุ่ม (random error) ภายใต้เงื่อนไขที่ถูกระบุไว้ของการวัด
การประเมินและยอมรับผลการตรวจสอบความใช้ได้ของความเที่ยงของวิธีวิเคราะห์ ดำเนินการได้ดังนี้
1) ทำการทดสอบตัวอย่างซ้ำในช่วงความเข้มข้นที่ครอบคลุมช่วงการใช้งาน ความเข้มข้นละ 10 ซ้ำ (ไม่น้อยกว่า 7 ซ้ำ)
2) ทดสอบอย่างน้อย 3 ความเข้มข้น คือความเข้มข้นต่ำ กลาง สูง หรือระดับความเข้มข้นที่ LOQ (ถ้ามีการหา LOQ) และหรือ 0.5 เท่า 1.0 เท่า 1.5 เท่า (หรือ 2.0 เท่า) ของค่าความเข้มข้นที่กำหนด (target concentration)
3) คำนวณค่า standard deviation (s) หรือ relative standard deviation (RSD)
4) นำค่าที่ได้ไปเทียบกับเกณฑ์ที่กำหนด ให้เลือกวิธีใดวิธีหนึ่ง ดังนี้
วิธีที่ 1 เกณฑ์การยอมรับที่ถูกกำหนดไว้แล้ว ได้แก่ ข้อกำหนดตามกฎหมาย ข้อกำหนดตามวิธีมาตรฐาน หรือค่าแนะนำสำหรับการยอมรับ ดังตารางที่ 5
ตารางที่ 5 ค่าแนะนำสำหรับการยอมรับความเที่ยงของสารที่สนใจที่ระดับความเข้มข้นต่าง ๆ
| ปริมาณสารที่สนใจ (%) | อัตราส่วนสารที่สนใจ | หน่วย | RSD (%) | ร้อยละการกลับคืนเฉลี่ย |
| 100 | 1 | 100% | 1.3 | 98-102 |
| 10 | 10-1 | 10% | 2.8 | 98-102 |
| 1 | 10-2 | 1% | 2.7 | 97-103 |
| 0.1 | 10-3 | 0.1% | 3.7 | 95-105 |
| 0.01 | 10-4 | 100 ppm | 5.3 | 90-107 |
| 0.001 | 10-5 | 10 ppm | 7.3 | 80-110 |
| 0.0001 | 10-6 | 1 ppm | 11 | 80-110 |
| 0.00001 | 10-7 | 100 ppb | 15 | 80-110 |
| 0.000001 | 10-8 | 10 ppb | 21 | 60-115 |
| 0.0000001 | 10-9 | 1 ppb | 30 | 40-120 |
ที่มา: Huber, L. Validation and Qualification in Analytical Laboratories, 2007, p.144-146.
วิธีที่ 2 การประเมินผลตามสมการของ Horwitz วิธีนี้ให้นำค่า RSD จากการทดสอบซ้ำมาเปรียบเทียบกับ RSD จากการคำนวณในสมการของ Horwitz ซึ่งสมการ Horwitz พบว่า RSD สัมพันธ์กับ log concentration แสดงภาพที่ 2 โดยที่การทดสอบซ้ำจากหลายห้องปฏิบัติการ พบความสัมพันธ์ว่า RSD = ±2(1-0.5 logC) และการทดสอบซ้ำภายในห้องปฏิบัติการเดียวกันจะมีค่า RSD อยู่ที่ 2 ใน 3 (~0.66) ของการทดสอบจากหลายห้องปฏิบัติการ โดยสรุปเป็นสมการ Horwitz ดังนี้
วัดซ้ำจากห้องปฏิบัติการหลายแห่ง RSDR = ±2C-0.1505
วัดซ้ำจากห้องปฏิบัติการเดียวกัน RSDr = ±(0.66)(2)C-0.1505
เมื่อ C = อัตราส่วนความเข้มข้น (concentration ratio)
จากสมการเมื่อคำนวณ RSD ที่ความเข้มข้นต่าง ๆ จะได้ค่า predicted Horwitz ดังตารางที่ 6
ตารางที่ 6 ความสัมพันธ์ระหว่างค่าความเข้มข้นกับ predicted Horwitz
| ความเข้มข้น | Conc. Ratio:C | Predicted Horwitz | |
| RSDR | RSDr | ||
| 100% | 1 | 2.0 | 1.3 |
| 10% | 0.1 | 2.8 | 1.9 |
| 1% | 0.01 | 4.0 | 2.6 |
| 0.1% | 0.001 | 5.7 | 3.7 |
| 0.01% | 0.0001 | 8.0 | 5.3 |
| 10 ppm | 0.00001 | 11.3 | 7.5 |
| 1 ppm | 0.000001 | 16.3 | 10.6 |
| 10 ppb | 0.0000001 | 22.6 | 14.9 |
RSDR คือการทดสอบซ้ำจากห้องปฏิบัติการหลายแห่ง
RSDr คือการทดสอบซ้ำจากห้องปฏิบัติการเดียวกัน
เกณฑ์การยอมรับความเที่ยงตามสมการ Horwitz
1) ค่า RSD จากการทดลองต้องน้อยกว่า RSD จากสูตรในการคำนวณตามสมการ Horwitz
2) ถ้าค่า RSD จากการทดลองมากกว่า RSD จากสูตรในการคำนวณตามสมการ Horwitz ให้หาค่า HORRAT จากสูตร
เมื่อ RSDex = experimental RSD
RSDpr = predicted RSD
- ค่าที่ยอมรับ HoR ต้องอยู่ระหว่าง 0.5 – 1.5
- AOAC ยอมรับ HoR น้อยกว่าหรือเท่ากับ 2
- EU, Codec ยอมรับ HoR น้อยกว่า 2
ความเที่ยงเป็นปัจจัยพิจารณาที่สำคัญโดยเฉพาะเมื่อต้องเกี่ยวข้องกับขั้นตอนการเตรียมตัวอย่าง ซึ่งอาจกระทบต่อความแม่นของการวิเคราะห์ได้ การทำซ้ำได้ของการวัดของการวิเคราะห์จะลดลงเป็นสัดส่วนโดยตรงกับระดับความความเข้มข้นของสารที่สนใจที่น้อยลง ความสัมพันธ์ดังกล่าวแสดงได้ในภาพที่ 2 ความไม่แน่นอนในการวิเคราะห์สารปริมาณน้อย ๆ (trace analysis) จะเพิ่มขึ้นอย่างชี้กำลัง (exponential) เมื่อเทียบกับการวิเคราะห์สารในระดับความเข้มข้นสูง
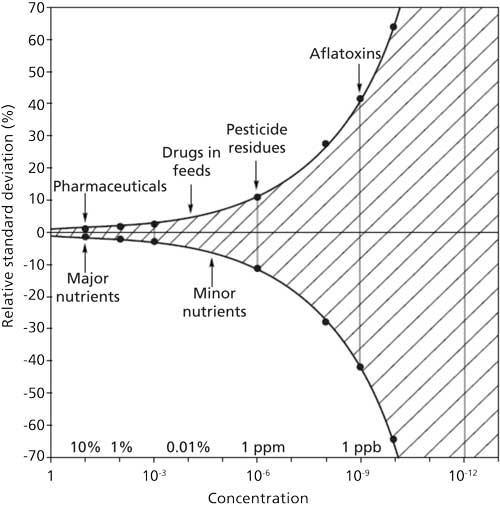
ภาพที่ 2 ความสัมพันธ์ของ Horwitz’s Curve (Horwitz trumpet). ดัดแปลงจาก Minimizing the effect of sample preparation on measurement uncertainty. โดย Meyer, 2002, p.106–112.
ความสัมพันธ์เชิงเส้นตรง (linearity) หรือช่วงความเป็นเส้นตรง (linear range) เป็นคุณลักษณะเฉพาะของวิธีทดสอบที่แสดงความสัมพันธ์อย่างเป็นสัดส่วนโดยตรงระหว่างปริมาณที่ทราบค่ากับปริมาณจากการวัด (สัญญาณตอบสนอง) ความสัมพันธ์เชิงเส้นตรงแสดงความสามารถของวิธีที่ให้ค่าสัญญาณของเครื่องมือวัดที่เป็นสัดส่วนโดยตรงกับความเข้มข้นของสารที่สนใจ การหาความสัมพันธ์เชิงเส้นตรง จำเป็นต้องมีการตรวจสอบสำหรับวิธีที่มีช่วงการทดสอบหรือช่วงการใช้งานที่กว้าง โดยต้องประเมินตลอดช่วง (range) ที่ระบุสำหรับการวิเคราะห์ การตรวจสอบความสัมพันธ์เชิงเส้นตรงทำได้ 2 แนวทางคือ
1) ความสัมพันธ์เชิงเส้นตรงของเครื่องมือ (system linearity) เป็นคุณลักษณะที่แสดงความสมพันธ์อย่างเป็นสัดส่วนโดยตรงระหว่างสัญญาณจากเครื่องมือวัด (response) และความเข้มข้นของสารในช่วงของการใช้งาน โดยใช้กราฟมาตรฐาน (calibration curve) โดยตามทฤษฎีแล้วความสัมพันธ์ระหว่างปริมาณกับสัญญาณจากเครื่องมือเป็นเส้นตรง ในการหาปริมาณความสัมพันธ์เชิงเส้นตรงของเครื่องมือเกี่ยวข้องกับสภาพไว และบางกรณีเกี่ยวข้องกับ matrix effect ด้วย
2) ความสัมพันธ์เชิงเส้นของวิธี (method linearity) เป็นความสัมพันธ์ระหว่างปริมาณของสารมาตรฐานที่วัดกับปริมาณที่วัดได้ ทดสอบโดยใช้วัสดุอ้างอิงรับรองหรือวัสดุอ้างอิงที่มีเนื้อสารเดียวกันหรือใกล้เคียงกับตัวอย่าง
ความสัมพันธ์เชิงเส้นตรงของกราฟเทียบมาตรฐานสำหรับการตรวจวัด (calibration curve) สร้างโดยการเขียนระหว่างระหว่างสัญญาณตรวจวัด (signal response) กับความเข้มข้นของสารมาตรฐาน ดังภาพที่ 3 ซึ่งความสัมพันธ์เชิงเส้นตรงคือช่วงความเข้มข้นของกราฟที่เป็นเส้นตรง
ภาพที่ 3 ความสัมพันธ์เชิงเส้นตรงของกราฟเทียบมาตรฐาน. ดัดแปลงจาก Validation and Qualification in Analytical Laboratories. โดย L. Huber, 2007, p.148.
เนื่องจากความสัมพันธ์เชิงเส้นไม่ใช้สมบัติเชิงปริมาณ หากการตรวจสอบพบว่าความสัมพันธ์ไม่เป็นเส้นตรง อาจสามารถแก้ไขได้ด้วยการใช้สมการอื่นหรือกำหนดช่วงให้แคบลงที่มีความสัมพันธ์เชิงเส้นตรง การหาความสัมพันธ์เชิงเส้นตรงของวิธีวิเคราะห์ใช้สำหรับวิธีที่ต้องใช้เครื่องมือในการวิเคราะห์ทำได้โดยเตรียมสารมาตรฐานที่มีระดับความเข้มข้นต่างกันอย่างน้อย 5 ระดับ เมื่อวัดสัญญาณจากเครื่องมือวิเคราะห์แล้วสร้างกราฟระหว่างค่าสัญญาณที่กับความเข้มข้นของสารมาตรฐาน การประเมินความสัมพันธ์เชิงเส้นตรงจะประเมินด้วยตา (visual inspection) ถ้ามีความสัมพันธ์เป็นเส้นตรง ให้คำนวณหา regression line โดยวิธีวิเคราะห์ความถดถอยเชิงเส้นตรง (least-square analysis) และหาสมการเส้นตรงของกราฟเทียบมาตรฐาน (calibration equation) ในรูป y = mx + c และหาสัมประสิทธิ์สหสัมพันธ์เชิงเส้น (correlation coefficient) ใช้สัญลักษณ์ r หรือ R หรือสัมประสิทธิ์ของการตัดสินใจ (coefficient of determination) ใช้สัญลักษณ์ r2 หรือ R2 ทั้งค่า R และ R2 แสดงความสัมพันธ์เชิงเส้นตรงของกราฟ โดยกราฟเส้นตรงที่ดีควร มีค่า R และ R2 ใกล้เคียง 1
ขีดจำกัดในการตรวจวัด (detection limit, LOD) หรือขีดจำกัดของเครื่องมือตรวจวัด (instrumental detection limit, IDL) คือค่าความเข้มข้นหรือปริมาณต่ำที่สุดของสารที่สนใจในสารตัวอย่างใด ๆ ที่เครื่องมือวิเคราะห์จะสามารถตรวจวัดได้ ซึ่งระดับความเข้มข้นดังกล่าวต้องมากกว่าค่าความไม่แน่นอนที่ประเมินได้ ตามข้อแนะนำของ ICH ได้ระบุในเอกสาร Q2(R1) กำหนดวิธีการหาค่า LOD มี 3 แบบดังนี้
- Based on visual evaluation คือการประเมินด้วยการมองเห็น โดยการวิเคราะห์ตัวอย่างที่ทราบความเข้มข้น และหาค่าต่ำสุดของตัวอย่างที่วิธีวิเคราะห์สามารถตรวดวัดได้
- Based on signal-to-noise วิธีนี้สามารถใช้กับเทคนิคที่ให้ baseline noise เช่น เทคนิค HPLC โดยทำการเปรียบเทียบ signal ที่วัดได้จากตัวอย่างที่รู้ความเข้มข้นต่ำของสารที่วิเคราะห์กับตัวอย่างที่เป็น blank เรียกว่า signal-to-noise ratio โดยทั่วไปสำหรับ LOD ค่าที่ยอมรับคือ 3 หรือ 2 ต่อ 1
- Based on the standard deviation of the response on the slope เป็นวิธีการหา LOD จากส่วนเบี่ยงเบนมาตรฐานของสัญญาณและความชันของกราฟมาตรฐาน จากสมการ
LOD = 3.3σ/s
เมื่อ σ คือ ส่วนเบี่ยงเบนมาตรฐานของสัญญาณ
s คือ ความชันของกราฟมาตรฐาน
จากภาพที่ 3 ค่า LOD กำหนดจากค่าความเข้มข้นของสารที่สนใจที่มีค่าสัญญาณตรวจวัด (signal) ที่อ่านได้จากเครื่องมือ เมื่อทำการทดสอบไร้สิ่งตัวอย่าง (blank test) หรือการวิเคราะห์แบลงก์ (blank) ซึ่งหมายถึงสารหรือสารละลายที่มีองค์ประกอบของสารตัวอย่างทั้งหมด ยกเว้นสารที่สนใจวิเคราะห์ และสัญญาณตรวจวัดนี้มีความแตกต่างจากสัญญาณรบกวน (noise) อย่างชัดเจน โดยเครื่องมือทุกชนิดจะมีสัญญาณรบกวนอยู่ด้วยเสมอ และจะมีมากหรือน้อยขึ้นอยู่กับคุณภาพของเครื่องมือวิเคราะห์นั้น ๆ ดังภาพที่ 4 โดยสัญญาณรบกวนหรือสัญญาณอิเล็กทรอนิกส์ คือความผันผวนของสัญญาณของเครื่องมือจากการวัดสัญญาณต่อเนื่องหรือตรวจวัดซ้ำหลาย ๆ ครั้ง และพิสัยของความผันผวนของสัญญาณอยู่ระหว่างระดับสูงสุดและต่ำสุดของสัญญาณ
ภาพที่ 4 กราฟของสัญญาณรบกวน (noise) และสัญญาณ (Signal) ของแบลงค์
วิธีการหา LOD ของวิธีทดสอบ
1) เตรียมตัวอย่างแบลงค์ (sample blank) 10 ขวด วัดค่าความเข้มข้นขวดละ 1 ครั้ง จากนั้นคำนวณค่าความเข้มข้นเฉลี่ย (mean) และค่าเบี่ยงเบนมาตรฐานของความเข้มข้น (standard deviation)
LOD = mean of sample blank value + 3s
2) เตรียมตัวอย่างแบลงค์ (sample blank) ที่ fortified ด้วยสารที่ต้องการวัดที่ความเข้มข้นต่ำ ๆ (lowest acceptable concentration) 10 ขวด วัดค่าขวดละ 1 ครั้ง จากนั้นคำนวณค่าเฉลี่ย (mean) และค่าเบี่ยงเบนมาตรฐาน (standard deviation) ของความเข้มข้นที่ fortified ลงไป
LOD = 0+3s
3) เตรียมตัวอย่างแบลงค์ (sample blank) ที่ fortified ด้วยสารที่ต้องการวัดที่ความเข้มข้นต่ำๆ (lowest acceptable concentration) 10 ขวด วัดค่าขวดละ 1 ครั้ง จากนั้นคำนวณค่าเฉลี่ย (mean) และค่าเบี่ยงเบนมาตรฐาน (standard deviation) ของความเข้มข้นที่ fortified ลงไป
LOD = mean of sample blank value + 4.65s
ในทางปฏิบัติการหา LOD ของวิธีทำได้โดยสร้างกราฟมาตรฐานหลายระดับความเข้มข้น เขียนกราฟระหว่างค่าความเข้มข้นกับสัญญาณที่วัดได้ จะได้สัญญาณรบกวน (noise) คือค่า intercept ของแกน y จากนั้นนำค่าสัญญาณรบกวน (noise) คูณ 3 (ตำราบางเล่ม คูณ 2) แล้วอ่านค่าความเข้มข้นจากกราฟมาตรฐาน ความเข้มข้นที่อ่านได้คือค่า LOD