ผู้ช่วยศาสตราจารย์ ดร.วรวิทย์ จันทร์สุวรรณ
ปรับปรุงล่าสุด : 26 พฤษภาคม 2563

เลขนัยสำคัญ...สำคัญไฉน?
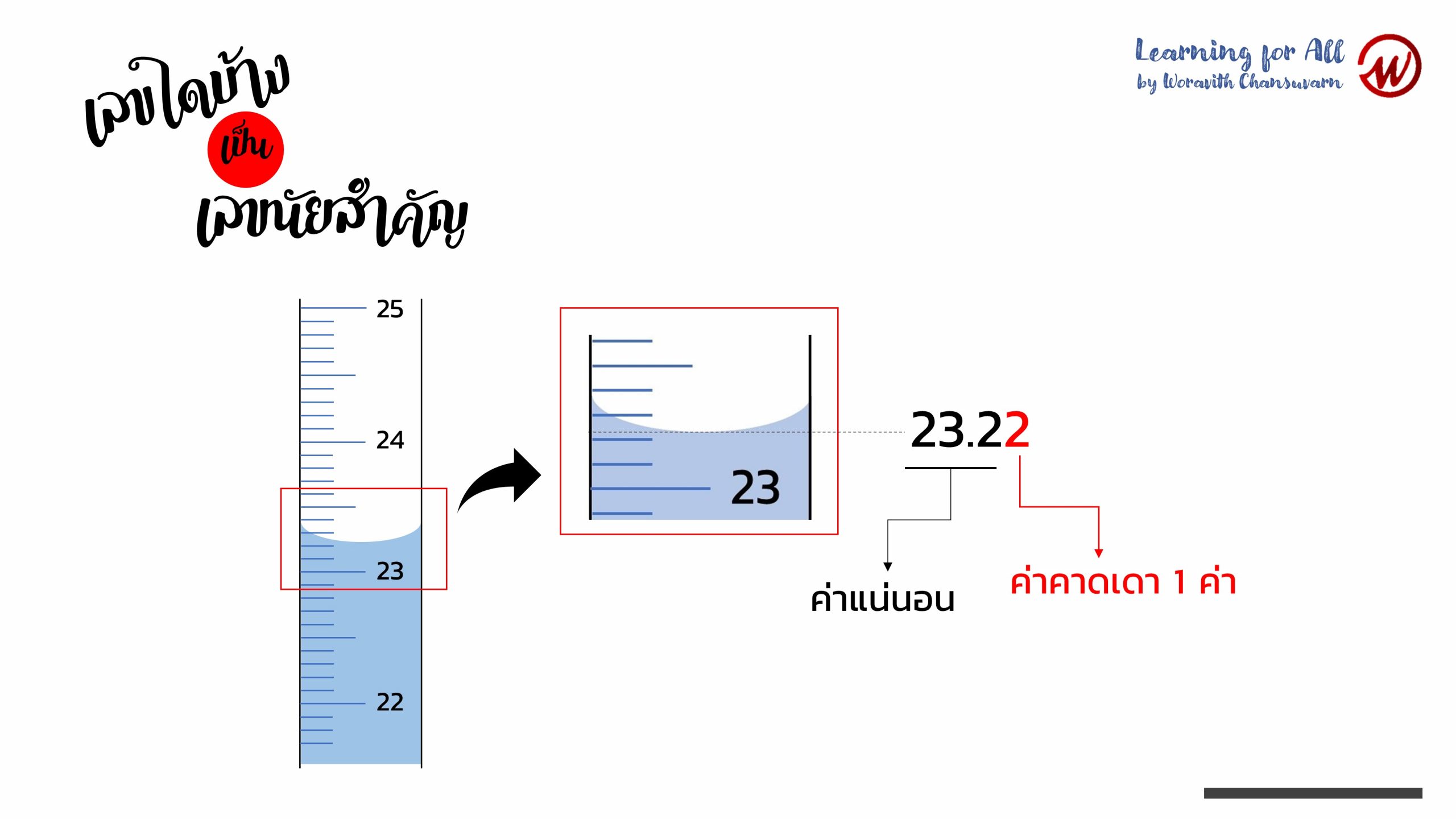
การบันทึกหรือรายงานผลการทดลองสำหรับการบอกจำนวนหรือปริมาณของสารที่เป็นค่าตัวเลข ตัวเลขที่แสดงนั้นต้องสามารถบอกถึงความถูกต้อง และ/หรือ ความเที่ยงของการวัดหรือเครื่องมือวัด ตัวเลขดังกล่าวนี้เรียกว่า เลขนัยสำคัญ (significant figure) โดยตัวเลขนัยสำคัญประกอบด้วยตัวเลขทุกตัวที่แสดงแน่นอน (certainty) รวมกับตัวเลขอีกตัวหนึ่งที่แสดงความไม่แน่นอน (uncertainty)
หลักการนับตัวเลขนัยสำคัญ
การนับตัวเลขนัยสำคัญ จะนับจากตัวเลขที่แน่นอนตัวแรกสุดที่ไม่ใช่เลขศูนย์ รวมถึงตัวเลขสุดท้ายที่มีค่าไม่แน่นอนอีกหนึ่งตัว
ตัวอย่างเช่น
- 2.76 มีตัวเลขที่แน่นอน 2 ตัว คือเลข 2 และ 7 และตัวเลขที่ไม่แน่นอนคือเลข 6 จึงมีจำนวนเลขนัยสำคัญ 3 ตัว
- 0.1084 มีตัวเลขที่แน่นอน 3 ตัว คือเลข 1 0 และ 8 และตัวเลขที่ไม่แน่นอนคือเลข 4 จึงมีจำนวนเลขนัยสำคัญ 4 ตัว (เลข 0 ตัวแรกไม่นับ)
ถ้ามีเลขศูนย์อยู่ระหว่างตัวเลขให้นับเลขนัยสำคัญด้วย เช่น
- 1.008 มีจำนวนเลขนัยสำคัญ 4 ตัว โดยมีเลข 1 0 และ 0 เป็นค่าที่แน่นอน และเลข 8 เป็นตัวเลขที่ไม่แน่นอน
- 0.501 มีจำนวนเลขนัยสำคัญ 3 ตัว เลข 5 และ 0 เป็นค่าที่แน่นอน และ 1 เป็นตัวเลขที่ไม่แน่นอน
- 0.0050003 มีจำนวนเลขนัยสำคัญ 5 ตัว เลข 5 และ 0 อีก 3 ตัว ที่อยู่ถัดไปเป็นค่าที่แน่นอน และ 3 เป็นตัวเลขที่ไม่แน่นอน
หลักการปัดเลขนัยสำคัญ
การปัดเลข ในการปัดตัวเลขให้พิจารณาตัวเลขที่ตามหลังตัวเลขนัยสำคัญตัวสุดท้าย
2.1) ถ้าตัวเลขที่พิจารณามีค่ามากกว่าเลข 5 ให้ปัดขึ้น เช่น 2.78 ต้องการเลขนัยสำคัญเพียง 2 ตัว โดยการตัดเลข 8 ออก เนื่องจากเลข 8 มีค่าสูงกว่า 5 ให้ปัดขึ้น จะได้เป็น 2.78 = 2.8
2.2) ถ้าตัวเลขที่พิจารณามีค่าน้อยกว่าเลข 5 ให้ปัดทิ้ง เช่น 2.72 ต้องการปัดเลข 2 ออกให้ตัดทิ้งจะได้เป็น 2.7
2.3) ถ้าตัวเลขที่พิจารณาเป็นเลข 5 ให้พิจารณาดังนี้
- ตัวเลขนำหน้า 5 เป็นเลขคู่ (หรือเป็น 0) ให้ตัดเลข 5 ทิ้งไป เช่น 2.85 = 2.8
- ตัวเลขนำหน้า 5 เป็นเลขคี่ ให้ปัดเลข 5 ขึ้น เช่น 2.75 = 2.8
หลักการคำนวณเลขนัยสำคัญ
1) ตัวเลขนัยสำคัญที่ได้จากการบวกหรือลบ ผลลัพธ์ต้องมีเลขทศนิยมเท่ากับจำนวนเลขที่อยู่หลังจุดทศนิยมที่มีจำนวนน้อยที่สุด เช่น
12.45 + 134.324 + 60.4786 = 207.2526
ดังนั้นผลลัพธ์ต้องมีเลขทศนิยมเท่ากับสองตำแหน่ง เราต้องนำหลักการปัดเลขมาพิจารณาเลข 5 ซึ่งหลังเลข 5 เป็น 2 ซึ่งน้อยกว่า 5 ดังนั้นให้ปัดทิ้ง คำตอบที่ถูกต้องตามหลักเลขนัยสำคัญคือ 207.25
2) ตัวเลขนัยสำคัญที่ได้การคูณหรือหาร ผลลัพธ์ที่ได้ต้องมีเลขนัยสำคัญเท่ากับตัวเลขที่นำมาคูณหรือที่มีจำนวนเลขนัยสำคัญน้อยที่สุด เช่น
0.90815 = 0.91
ดังนั้นผลลัพธ์ต้องมีเลขนัยสำคัญเท่ากับตัวเลขที่นำมาคูณหรือที่มีจำนวนเลขนัยสำคัญน้อยที่สุด นั่นคือ 5.2 (นับเลขนัยสำคัญได้ 2 ตัว) เราต้องนำหลักการปัดเลขมาพิจารณาเลข 0 ซึ่งหลังเลข 0 เป็น 8 ซึ่งมากกว่า 5 ดังนั้นให้ปัดขึ้น คำตอบที่ถูกต้องตามหลักเลขนัยสำคัญคือ 0.91
3) ตัวเลขที่ได้จากคำนวณเกี่ยวกับลอการิทึม (logarithm) เช่นการเปลี่ยนลอการิทึมไปเป็น antilogarithm หรือเปลี่ยนกลับกัน การหาค่าลอการิทึมของตัวเลขจำนวนหนึ่งค่าที่ได้ประกอบด้วยตัวเลขสองชนิดคือ characteristic และ mantissa การนับเลขนัยสำคัญจะนับจำนวนเลขที่เป็น mantissa เท่านั้นให้มีจำนวนเลขนัยสำคัญเท่ากับตัวเลขนัยสำคัญที่นำมาหาค่าลอการิทึม

log (1.35x104) = 4.130
เช่น log x = 13.1769
x = 1.530x1013
ตัวอย่าง
จงคำนวณค่าต่อไปนี้ตามหลักเลขนัยสำคัญ
1) 4.65x1.4 = 6.51 = 6.5
2) 36.45 + 1.467 = 37.917 = 37.92
3) 105.36/2.31 = 46.61038961 = 46.6
4) -log 1.75x10-5 = 4.75696 = 4.757